A Break - WEEK 13 : Hello There 👀 & Game Math
[DEVLOG] Week 13
A Break
No Patch This Week
I have been a bit distracted with other IRL things this last week.
I can no longer promise weekly patches, but I can keep the devlog's coming at the very least.
Fear not! I do still plan to finish this game project! 👀
The other contributors have also been a bit busy or on a vacation.
Right now, we are trying to figure out the content after the Beacon and started flirting a bit with the game lore & endings.
Feel free to join our Discord - add tiny_takin_teller for an invite 👀
A Bit Of Game Math
Game Version is [Prototype : Week 12]
For conventional idle games, see The Math Of Idle Games.
But this game scales a bit unconventionally. Currently, there are no limiting factors like in most incremental games (no resource storage capacity, no increasing costs, ...). So, the game starts scaling exponentially rather quickly.
QUESTION: What is the fastest possible time to reach the "Infinite" amount of peasants?
Currently, the game storage limit is set at 10^18 which is near the magnitude of the 64-bit computing limit. For all intents and purposes, currently the game does not implement larger values and considers this "Infinite" amount of items.
For simplicity, lets say you ignore growing Swordsmen and other types of resources, and focus only on maximizing the growth of the Peasants.
Each Mason produces one House per game's "population cycle", while each House grants 4 more population slots.
To keep resources balanced, every 1 additional Mason needs 105 additional workers:
- 45 peasants
- 22 lumberjack
- 5 stone miner
- 10 clay digger
- 10 clay baker
- 7 hunter
- 2 coal miner
- 2 torch man
- 2 explorer
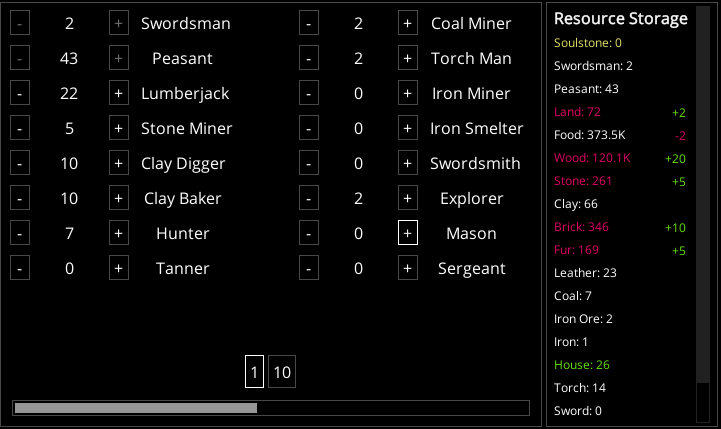
That is, for every 106 additional population slots, we can support one additional Mason among them.
Lets say we start at a point where we can support the 1st Mason, producing 4 population per cycle. Then, we need:
- 106 / 4 = 26.50 additional cycles to support 2nd Mason
- 106 / 8 = 13.25 additional cycles to support 3rd Mason
- 106 / 12 = 8.83 additional cycles to support 4th Mason
- 106 / 16 = 6.63 additional cycles to support 5th Mason
- ...
- 106/108 = 0.98 additional cycles to support 28th Mason (at this point, gaining 1 Mason per cycle)
- ...
- 106/212 = 0.5 additional cycles to support 54th Mason (at this point, gaining 2 Mason per cycle)
- ...
For supporting m-th Mason (m > 1), we need 106/[4(m-1)] additional cycles.
That is, the number of cycles N elapsed since getting M Masons will be the sum:
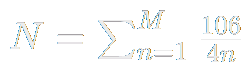
This can be approximated with the harmonic series as

We can then plug in our numbers into this
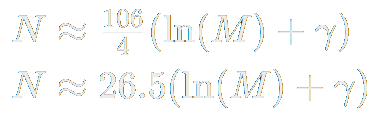
Inverting this expression, gives us the formula for number of Masons after N cycles
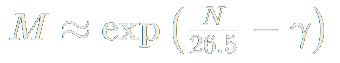
We can equate this with "M = 10^18 / 106" to get the number of cycles after our population slots reach "Infinity", given this strategy of maximizing Mason production.
This assumes that the player is fast enough to properly distribute all new population slots each cycle, an idealized scenario...
This gives us the result of 990.048 cycles. Since each cycle is 5 seconds currently, this means the answer to the QUESTION is 82.5 minutes! (This does not account time needed to acquire the 1st Mason.)
P.S. a more realistic scenario is for a player to spend most of their time AFK and then distribute new population slots at certain intervals. The player would also spend some population slots on other resources and on progressing Swordsmen.
Then, we get calculations that estimate anywhere between a whole day to more than a whole week... of combined AFK & Active play styles, to reach "Infinite" amount of resources.
A Dark Forest
Incremental Minimalistic Idle Game
| Status | Prototype |
| Authors | TinyTakinTeller, Abyssal Novelist |
| Genre | Adventure |
| Tags | 2D, Godot, Incremental, Minimalist, No AI, Open Source, Short, Singleplayer, Text based |
| Languages | English, French, Polish, Portuguese (Brazil), Thai, Chinese, Chinese (Simplified) |
More posts
- 🌎 Language Update: Thai 🌎 (Patch 1.4.5)Jun 12, 2025
- Steam Next Fest June 2025 and Press Kit!Jun 09, 2025
- Steam Demo Release & Next Fest 2025Jun 06, 2025
- 🚀Patch 1.4 : 🎨The Art Update! + 🔮The Future +🌍Polish Localization!Feb 11, 2025
- * [Art][Paid] Looking For An ArtistJan 25, 2025
- ⚡ Patch 1.3 : Soulstone Grind FixJan 11, 2025
- 🌎 Language Update: Portuguese (Brazilian)Jan 08, 2025
- 🌎 Language Update: French & Chinese (SC)Jan 05, 2025
- 🚀 Prototype Release 1.0Oct 06, 2024
- Experiment - WEEK 20 : Mix New Game Genre?Sep 09, 2024
Leave a comment
Log in with itch.io to leave a comment.